During exam season, students in STEM disciplines will likely deny there is anything beautiful in their work. Their professors say otherwise.

Symmetrical, elegant, harmonious, unified: these are all words common in scientific discourse about experiments and equations, as well as the phenomena they relate to. Despite their shared language surrounding beauty, math and science are often distanced from philosophy and art, the disciplines usually associated with aesthetics. 

Perhaps this is because of the subjective, emotional element of aesthetic judgment, which is incompatible with the goal of scientific inquiry to explain objective truths about the natural world. Perhaps it results from the sterile environments scientists often inhabit — I think it’s safe to say that the narrow, fluorescent-lit corridors of Percival Stern Hall suffocate some aesthetic inclination.

Philosophers have long disputed the concept of beauty, but the general consensus is that it is neither wholly subjective or objective in nature. If beauty were entirely subjective, for instance, then the word would be drained of all the communicative value we understand it to have. By the same token, science is not entirely objective. There are a plethora of choices to be made during the process of scientific inquiry, which allows ample space for personal values and aesthetic motivations to come into play. The 20th-century theoretical physicist Paul Dirac was particularly bold in claiming that “it is more important to have beauty in one’s equations than to have them fit the experiment.”

In search of how beauty colors and shapes inquiry in STEM disciplines, I spoke to three Tulane professors — a biologist, a physicist and a mathematician — about their work. Here are their thoughts. 

***

Jennifer Fang is a biologist studying how blood vessels grow and organize in the development of healthy and diseased tissue. Her lab uses both in vivo and artificial microphysiological organ-on-a-chip models to study cells of the vascular system. 

What drew her to biology? The possibility of “appreciating the natural complexity” of “these very complex systems in our bodies,” she said, “all working in synchrony in order to be able to maintain what is ultimately a very vulnerable balance of health and life.” 

Organization and complexity became a major theme of our conversation.

“Every moment of our lives is us basically fighting against the natural erosion of all our energy states, and all of the systems that keep us alive trend towards inertness and death,” Fang said. “And part of being able to do that and be alive is to apply organization in a disorganized system.” 

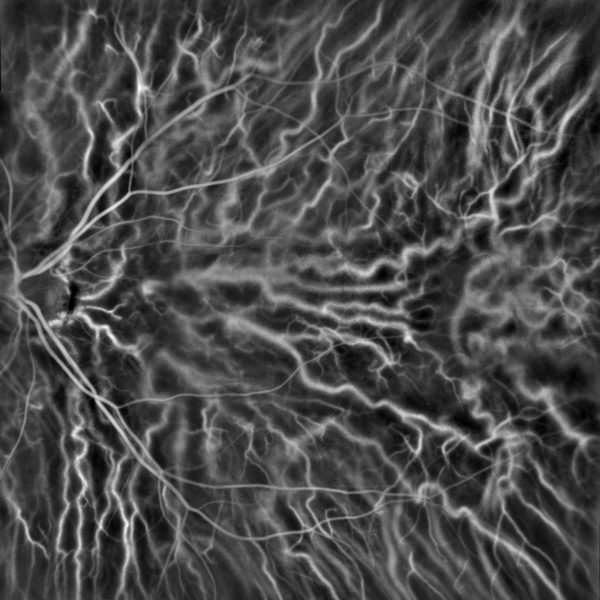
In one sense, Fang echoes a classical conception of beauty. As Aristotle wrote in his “Poetics,” “a beautiful object, whether it be a living organism or any whole composed of parts, must not only have an orderly arrangement of parts, but must also be of a certain magnitude.” In framing biological systems as engaged in a doomed fight against entropy, she also suggested a kind of narrative, tragically-structured beauty that occurs all the way down. But Fang also acknowledged that, at times, beauty requires more than being able to reduce a complex system to a comprehensible one — sometimes, it involves a self who, in face of such a vast system, looks at it simply in awe.

“Sometimes you’re not nerding out,” Fang said. “You just kind of step back and are like, ‘That is beautiful.’ That is art, because it evokes that same sort of pondering about who we are and our relationship with the universe.”

While it was organization and complexity for the biologist, the focus was symmetry and simplicity for Nick Sparks, a mathematical theoretical physicist studying the rotation of atomic nuclei. Like many physicists, he also has a penchant for philosophy; in fact, what drew him to physics was the fact that “it’s the closest thing to philosophy.”

Just as his studies in physics gradually developed out of philosophical questions, his intuitions about beauty in physics developed over time. Acknowledging the esoteric nature of mathematical beauty, he said, “It took me several years, or maybe more than several years, to appreciate the beauty of the equations. But [beauty] is a guiding principle in the sense that I feel like I’ve done my job if there’s a symmetry or if there’s something beautiful about things, and there’s a simplicity.”

Beauty and truth, then, are not the same for Sparks. Rather, beauty — or symmetry — has a regulative and predictive role in arriving at truths, which is a consequence of the top-down modeling approach to theoretical physics. “We build symmetry into our models, and then they work swimmingly,” Sparks said.

But what of the possibility that what we aesthetically appreciate is not the phenomena themselves, but our models of them? This seemingly trifling question actually has serious ramifications; some physicists have argued that searching for beauty in one’s equations stifles the progress of physics. In response to this concern, he framed model-building as an artistic craft and, recalling Friedrich Nietzsche in “Beyond Good and Evil,” emphasized the reciprocal relationship between artist and art. 

“It’s like a form of self expression,” Sparks said. “We put ourselves into these equations almost, and we put ourselves in the way that we model things. And that, in turn, puts something into us as well.” 

He concluded: “I think that physics or math even might become a high form of art.”

The mathematician I spoke to, Olivia Beckwith, was more hesitant in her claims about mathematics as art. A number theorist, her specific objects of study are modular forms, which, simply put, are functions with an infinite number of internal symmetries. The properties that come along with their symmetry makes them extremely powerful — they were used in the 1990s to prove Pierre de Fermat’s Last Theorem — are also showing promise in the development of the Langlands program — mathematics’ “theory of everything.” They are stunning as visual objects to boot.

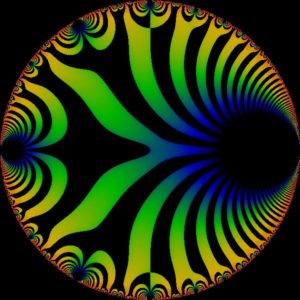
For Beckwith, it was the aesthetics of this area of math that initially drew her to it: “I think for most mathematicians going into abstract theoretical areas, they’re going to be more motivated by aesthetics than utility in general, and I definitely was.”

Nowadays, though, utility or something similar to it seems to play a larger part in Beckwith’s aesthetic judgments. In other words, it is not because modular forms are uniquely enigmatic that she finds them beautiful — as most non-mathematicians likely would — but because they are abstract and generic in a way that is ultimately useful in bringing new truths to light.

“I think one of the most beautiful things in math is when we build up all this abstract theory, and then nice equations — things that are not obvious without the theory — just fall very effortlessly out of those abstract principles,” she said. 

We might call this aesthetic criteria convergence and unity. Interestingly, the way these criteria manifest themselves visually seemed secondary to Beckwith. At one point, she drew a divide between visual aesthetics and the true beauty of mathematics, a beauty that is not immediately available or comprehensible. 

“I think there’s a difference between just looking at a beautiful picture and not necessarily knowing anything about what went into that picture … [and] what a lot of mathematicians enjoy in their work, like getting the story behind the theorem,” she said. 

Mathematical beauty, especially of objects in isolation, cannot be passively absorbed, according to Beckwith. Numbers themselves, who maybe possess a kind of statuesque beauty in their coldness and austerity, are given a new beauty, a kind of life, only through manipulations and associations.

“It’s an important point,” Beckwith said. “Not just seeing them as numbers, but seeing what’s going on behind them, that makes math really beautiful.”